Definicja wektora
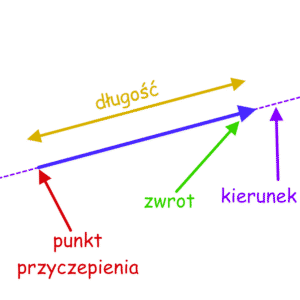
W artykule o jednostkach wspomniałem, że niektóre wielkości fizyczne nie można w pełni opisać wyłącznie za pomocą liczby i jednostki. W tym celu prowadzamy pojęcie wektora, który możemy utożsamić ze strzałką. Wektory, oprócz długości, cechują się również ułożeniem w przestrzeni. Mówimy, że wektor ma punkt zaczepienia, kierunek oraz zwrot. Graficznie widać to na poniższym rysunku. Na wektorach możemy wykonywać działania, takie jak dodawanie i mnożenie, które przedstawię w dalszej części tego wpisu.
Dodawanie wektorów
Dodawanie wektorów polega w istocie na dodaniu do siebie odpowiednich współrzędnych, jednak w fizyce dużo częściej spotkamy się z sytuacją, w której chcemy dodać wektory geometrycznie. Wykonujemy to za pomocą tzw. reguły równoległoboku, którą przedstawiłem na poniższym rysunku.
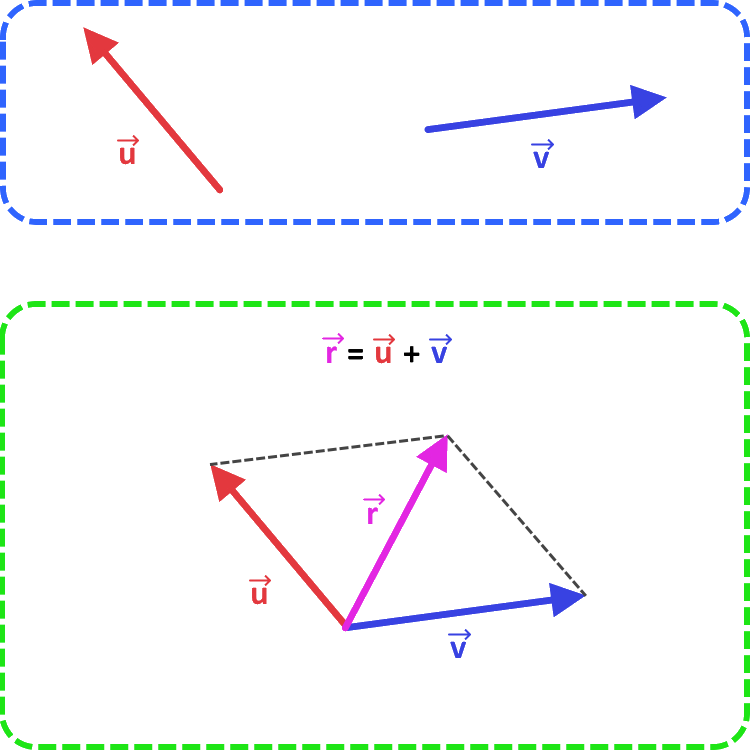
Aby dodać wektory \( \overrightarrow{u} \) i \( \overrightarrow{v} \):
- Narysuj oba wektory tak, że zaczynają się one w tym samym punkcie.
- Wyobraź sobie, że tworzysz równoległobok, którego bokami są te dwa wektory.
- Przekątna równoległoboku, wychodząca z punktu, w którym oba wektory się zaczynają, to suma tych wektorów.
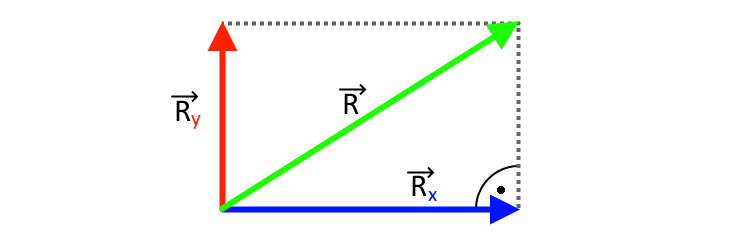
Często w zadaniach i różnych problemach przydatne okazuje się rozłożenie wektora na składowe, czyli dwa wektory prostopadłe do siebie, których suma jest rozkładanym wektorem. Na poniższym przykładzie składowe wektora \( \overrightarrow{R} \) poziomą i pionową oznaczyłem kolejno indeksami „x” i „y”.
Mnożenie wektora przez skalar
Wiemy już, czym jest skalar. Możemy dostrzec powiązanie tej nazwy ze skalowaniem i okazuje się, że nie jest ono przypadkowe. Jeśli chcemy coś przeskalować, np. balon albo okrąg, to możemy wyobrazić to sobie tak, jakbyśmy go „rozdmuchiwali”. Podobnie jest z mnożeniem wektora przez skalar. W wyniku tej operacji kierunek wektora oraz punkt przyczepienia pozostają bez zmian. Zmienia się długość wektora z wyjątkiem trywialnego przypadku mnożenia przez 1. Gdy skalar ma wartość ujemną, zwrot zmieniamy na przeciwny. Podsumowując, w wyniku przemnożenia wektora przez skalar otrzymujemy nowy wektor o niezmienionym kierunku i długości powiększonej tyle razy, ile wynosi wartość skalara. Zwrot zmienia się na przeciwny, jeśli wartość skalara jest ujemna.
Mnożenie wektorów na dwa sposoby
W fizyce spotkamy się z dwoma różnymi sposobami mnożenia wektorów. W zależności od rodzaju mnożenia, otrzymamy wektor albo skalar. Stąd właśnie biorą się nazwy tych operacji — iloczyn skalarny oraz iloczyn wektorowy.
Skoncentrujmy się teraz na iloczynie skalarnym. Jak sama nazwa wskazuje, w wyniku otrzymamy skalar. Iloczyn skalarny dwóch wektorów \( \overrightarrow{a} \) i \( \overrightarrow{b} \) zapisujemy następujaco: \( \overrightarrow{a} \circ \overrightarrow{b} = ab \cdot \cos{(\angle (\overrightarrow{a},\overrightarrow{b}))} \). Przez \( a \) oznaczamy długość wektora \( \overrightarrow{a} \), natomiast \( \angle (\overrightarrow{a},\overrightarrow{b}) \) to kąt pomiędzy kierunkami wektorów \( \overrightarrow{a} \) i \( \overrightarrow{b} \). Obecność cosinusa możemy wytłumaczyć tak, że dowolny z tych wektorów rozkładamy na wektory składowe[b]. Oznacza to, że wyobrażamy sobie, że istnieją dwa prostopadłe wektory składowe tego wektora, przy czym jeden z tych składowych wektorów ma kierunek drugiego wektor. Cosinus pozwala nam otrzymać wartość składowej równoległej do drugiego wektora. Inaczej mówiąc, iloczyn skalarny jest równy iloczynowi długości składowych o tym samym kierunku.
Przejdźmy do iloczynu wektorowego. Jak sama nazwa wskazuje, w wyniku mnożenia wektorowego otrzymujemy wektor. Co więcej, jest on prostopadły do płaszczyzny wyznaczonej przez mnożone wektory. Zanim przejdziemy do algebraicznego zapisu iloczynu wektorowego, to zwróćmy uwagę na fakt, że nowy wektor może mieć dwa różne zwroty. Zastanówmy się, jakie niesie to konsekwencje. Przypomnijmy sobie, że przy iloczynie skalarny kolejność mnożenia wektorów nie miała znaczenia, ponieważ wynik tego działania był skalarem. Skoro możemy otrzymać dwa wektory o różnych zwrotach (ale tych samych długościach i kierunkach) i mnożenie dwóch wektorów możemy zapisać na dwa sposoby, to kolejność wektorów występujących w iloczynie wektorowym będzie miała znaczenie. Mówimy, że iloczyn wektorowy jest nieprzemienny.
Iloczyn wektorowy \( \overrightarrow{a} \) i \( \overrightarrow{b} \) zapisujemy w następujący sposób: Iloczyn wektorowy \( \overrightarrow{a} \) i \( \overrightarrow{b} \) zapisujemy w następujący sposób: \( \overrightarrow{a} \times \overrightarrow{b} = ab \cdot \sin{\angle (\overrightarrow{a},\overrightarrow{b})} \)
Obecność sinusa możemy interpretować w ten sposób, że rozkładamy któryś z wektorów na składowe i bierzemy tę składową, która jest prostopadła do nierozłożonego wektora[b].
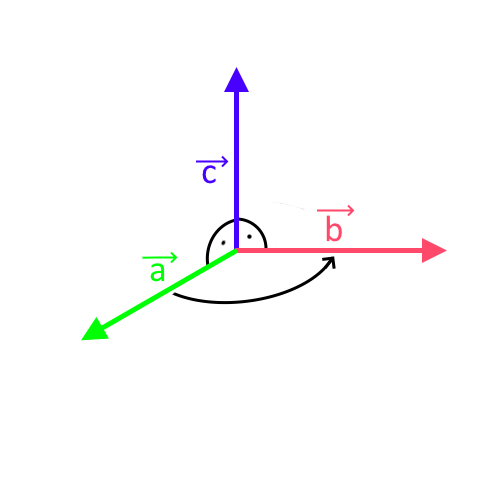
- Ustaw prawą dłoń tak, że wszystkie palce oprócz kciuka wskazują zwrot wektora \( \overrightarrow{a} \).
- Zegnij wszystkie palce oprócz kciuka tak, aby ich kierunek był zgodny z wektorem \( \overrightarrow{b} \).
- Wyprostowany kciuk wyznacza zwrot wektora \( \overrightarrow{c} \).
[a] Wracamy do dodawania wektorów. Podczas uczenia się fizyki często będziemy wracać do tego, czego już się nauczyliśmy. Jest to wyzwanie, gdyż bez solidnych podstaw można się pogubić w kolejnych działach.
[b] Co ciekawe, tutaj wybór wektora, który rozłożymy na składowe nie ma znaczenia, bowiem nie wpływa to na zwrot wektora powstałego z iloczynu wektorowego