Po co fizykom jednostki?
W fizyce zajmujemy się matematycznym opisaniem rzeczywistości wokół nas. W tym celu chcemy zmierzyć wielkości fizyczne, czyli pewne cechy i właściwości obiektów wyrażone ilościowo. Pojawia się jednak pewien problem, a mianowicie potrzebujemy pewnego wzorca, miary wzorcowej. W przeszłości za wzorce jednostek miar używano rozmaitych zjawisk i obiektów. Dla przykładu na Bliskim Wschodzie za wzorzec masy w handlu używano ziaren pewnej rośliny jako wzorca karata, a sekundę definiowano za pomocą ruchu obiegowego Ziemi. Ale rośliny, czy też inne procesy jak okres orbitalny Ziemi wokół Słońca mają pewien rozrzut, a przecież wzorzec ustalamy po to, aby był on jak najdokładniej określony. Istniał również inny problem, jakim były regionalne systemy jednostek na świecie.
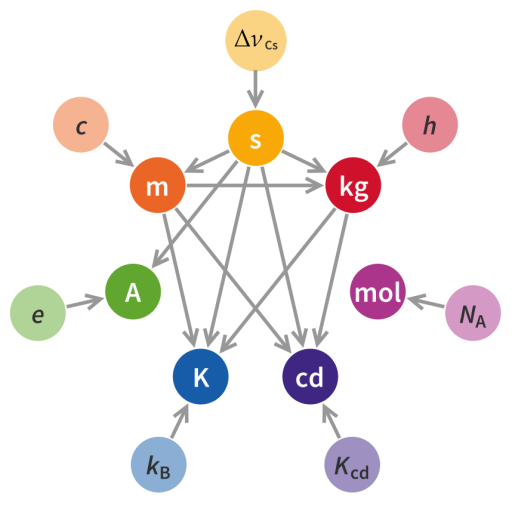
Próbę rozwiązania tych problemów stanowi układ jednostek SI, który jest używany w znacznej większości państw na świecie, a tzw. wielkości podstawowe są określone za pomocą zdefiniowanych wartości stałych fizycznych. Sekundę określamy jako 9 192 631 770[a] okresów nadsubtelnego przejścia w atomie cezu-133 w niezaburzonym stanie podstawowym. Przyjmujemy również prędkość światła, stałą Plancka, stałą Boltzmanna, ładunek elementarny oraz liczbę Avogadra za ustalone stałe. Pozwala nam to zdefiniować pozostałe jednostki jak metr, kilogram, amper, kelwin, czy mol. Możemy zwizualizować relacje pomiędzy jednostkami za pomocą poniższej grafiki.
Wielkości wektorowe, a skalarne
Tak jak wspomniałem, opisujemy różne wielkości fizyczne, które przecież również mają swoje cechy charakterystyczne.
Dla przykładu samo powiedzenie, że prędkość samochodu to 25\( \frac{m}{s} \) nie dostarcza nam żadnej informacji o tym, dokąd ten samochód jedzie. Nie wiemy, czy jedzie on na północ, czy południe, a może właśnie wjeżdża pod górę. Jednak bez problemu zauważamy, że w przypadku np. masy wystarczy nam liczba z jednostką np. 167 g. Nikt przecież nie pyta się nas, czy temperatura jest skierowana w dół, czy w lewo.
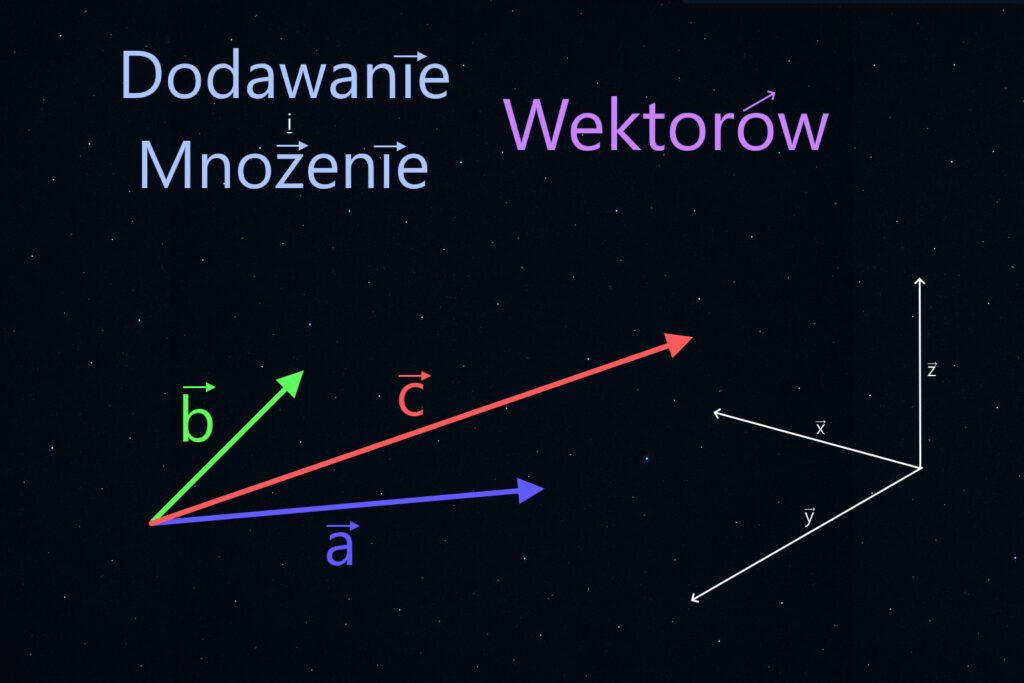
Stąd fizycy rozróżniają wielkości skalarne oraz wektorowe. W skrócie mówimy o wektorach i skalarach. Do opisu wielkości skalarnych wystarczy nam liczba i jednostka, tak jak w przykładzie wspomnianej masy, czy temperatury. Jeśli jednak mówimy o prędkości, przemieszczeniu, a nawet polu powierzchni[b], to te wielkości będziemy nazywać wektorowymi. Wektory mają długość, czyli wartość liczbową (tak jak skalary). Na tym podobieństwa się kończą, bo kolejne cechy są wynikają z ułożenia wektora w przestrzeni. W fizyce zwracamy uwagę, że wektor ma punkt przyczepienia. Zazwyczaj mamy na myśli tu nasadę strzałki, ale nic nie stoi na przeszkodzie, by za punkt przyczepienia uznać grot. Jest to właściwie równoważne, ponieważ wektory mają jeszcze dwie cechy, a mianowicie kierunek i zwrot. Kierunek to prosta w której zawiera się wektor, a zwrot jest określeniem strony, w którą jest on ustawiony.
Porada maturalna
Przy rozwiązywaniu zadań maturalnych należy pamiętać o podaniu wyniku wraz z jednostką. Jest to taki rodzaj błędu, który można łatwo uniknąć, a pomimo tego jest on częsty i na jego obecność zwrócono uwagę m.in. w oficjalnym raporcie dotyczącym matury z fizyki w roku 2024.
[a] Dziewięć miliardów sto dziewięćdziesiąt dwa miliony sześćset trzydzieści jeden tysięcy siedemset siedemdziesiąt.
[b]Tak, pole powierzchni możemy potraktować jak wektor. Bierze się to z tego, że w elektrostatyce oraz elektromagnetyzmie pojawią się pewne wielkości fizyczne, które nazwiemy strumieniami. Właściwie to, co rozumiemy przez strumień różni się od działu fizyki, ale w elektromagnetyzmie jest to miara tego, ile danej wielkości wektorowej, np. prędkości, przechodzi przez rozważany fragment powierzchni. Jeśli mamy obszar w którym poruszają się cząsteczki z pewnymi prędkościami w lewo i będziemy chcieli dowiedzieć się ile wynosi strumień prędkości w kierunku prostopadłym do tych prędkości, to jego wartość będzie różna od zera (o ile coś będzie się poruszać). Jeśli zbadamy strumień związany z powierzchnią równoległą do prędkości cząsteczek to strumień wyniesie 0.